西师版五年级上册第五单元《多边形面积的计算》
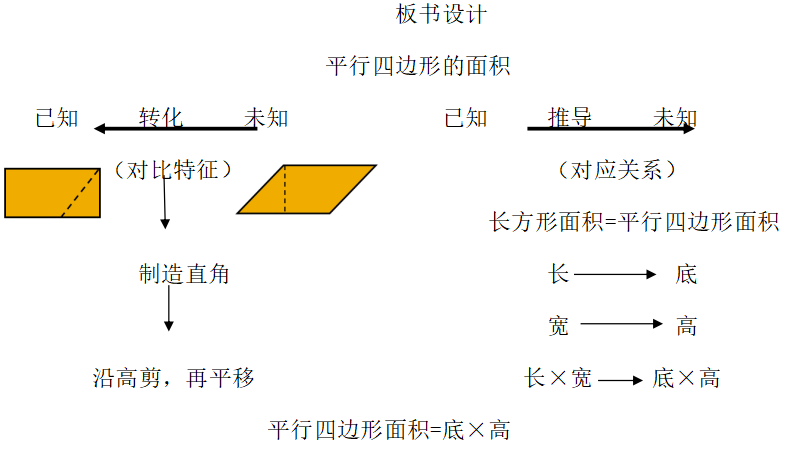
多边形面积的计算
第一课时(种子课:平行四边形的面积)
教学内容:西师版五年级上册79页
学生发展目标:
1.课时知识目标:会将平行四边形转化为长方形,并能讲清楚沿高剪的道理。能用简洁的语言讲清楚平行四边形面积公式推导的过程。
2.单元长程目标:通过对平行四边形面积公式的探究,获得探究多边形面积公式的一般思考路径。
3.核心素养目标:经历将平行四边形转化为长方形、利用长方形面积公式推导出平行四边形面积公式的过程,发展学生的直观想象能力和逻辑推理能力。
一、谈话引入,回顾转化思想
师:孩子们,世界上最早研究面积的是古埃及! 那他们为什么要去研究面积呢?请看(播放视频)
师:瞧,这就是他们划分好的农田,这些农田都有哪些形状?(抽生)
师:在这些平面图形中,哪些图形的面积是已经学习过的?(长方形、正方形)
师:对,长方形、正方形的面积是已知的,其余图形的面积计算方法暂时是未知的。
师:今天我们就借助平行四边形面积的研究,去探索多边形面积的奥秘。(板书课题)
二、对比特征,转化成长方形
师:平行四边形面积对我们来说是未知的,通常研究一个未知的新知识,我们采取什么方法?(板书:未知转化为已知)
师:你们准备把平行四边形转化成什么图形?长方形。(贴平行四边形,写长方形)
师:那怎样才能把平行四边形转化成长方形呢?
【自学要求】
请独立自学:转化图形
试一试:把平行四边形转化为长方形。
说一说:你是怎么把平行四边形转化成长方形的?
大家都有了自己的想法,接下来请组内交流。
【合作交流】
1.你是怎么把平行四边形转化成长方形的?
2.转化过程中要注意什么?
比如:你怎么保证转化后的图形就一定是一个长方形呢?
【个体展示汇报】
预设1:对着过顶点的高剪,
预设2:沿任意一条高剪
预设3:要垂直剪。(问:为什么要垂直剪,斜着剪行不行)
【师追问】
(1)怎么想到要沿高剪?(提示:沿高剪其实是想在这里得到什么?直角)
(突出:也就是长方形有4个直角,是长方形的特征:要沿高剪才能保证有直角,转化后一定是长方形。)(师适时板书“特征”)
(2)能不能两边各剪一个直角三角形,再把两个直角三角形不要了?
(突出:图形的转化,不能减掉一些扔了。要保证面积不变。)
【师小结】
我们一起来分析一下刚才转化的过程。可能有的同学转化是靠的直观感觉,感觉要沿着高剪;而有的同学说出了为什么要沿高剪。
其实我们要把平行四边形转化成长方形,就要对比这两个图形的特征,长方形有四个直角,平行四边形没有直角。(板书:对比特征(直角))
所以,我们就要去制造特征,制造直角,所以我们就想到了沿高剪。(板书:制造特征)
最后再通过图形的运动,比如通过平移,就实现了转化。(板书:图形的平移)
同学们现在清楚了吗?
【强化直观想象】
师:刚才每个同学只操作了一个平行四边形,其实平行四边形有很多,有大的小的,长的短的,胖的瘦的。现在请你们闭眼,在脑袋里想象一个平行四边形,然后用手比划着沿一条高剪开,再平移,拼成什么图形了?(拼成一个长方形)
请一起看一看大屏幕,跟你想象得一样吗?
结论:看来任意一个平行四边形都能转化为长方形。
三、新旧关联,推导面积公式
师:平行四边形那么多,如果每次遇到平行四边形都要转化后再去求面积,麻不麻烦。(麻烦)
那怎么办?(如果能得到一个算平行四边形的面积的公式就好了)
师:那接下来我们就来尝试公式的推导。通常我们进行公式推导是从已知推导到未知。你能不能利用已知的长方形面积公式推导出平行四边形的面积公式呢?(贴板书:已知—未知,长方形的面积,平行四边形的面积)
【自学要求】
独立尝试:推导公式
(1)独立自学(约3分钟)
1.观察转化前后的图形,找它们之间的关系,推导出平行四边形的面积公式。
2. 用简洁的语言或符号记录推导过程。(提示:拿出导学单)
师:大家都有了自己的思考,(抽一名学生)请你说说你是怎样推导的?
预设:刚才,这位同学说到了长方形的长、宽和平行四边形的底、高之间的关系,他在推到过程中抓住了各要素之间的关系。但他没有说到新旧图形的面积,你们认为转化前后图形的面积关系能忽略吗?看来,推导还需要关注面积关系,(板书:要素关系,面积关系)
师:看来要把推导过程说得有条理、说清楚,还有点困难。那到底要怎样才能有条理的说清楚呢,我们可以在小组合作中去试一试。
这一次,老师给大家提供了3个思维的路径,看一看是否对你有所启发。(请学生自己看一看,约1分钟)
师:看完了吗?现在请一个同学来读一读学习要求。
【互学要求】
1.组长主持,组员依次发言。
用简洁、有条理的语言,讲清楚公式推导的过程。
2.组内达成共识,派两名代表汇报。(一人主导说,一人配合演示)
【展学】
师:思维的碰撞能够激出知识的火花。哪个小组来展示。
师中途提示:孩子,能不能借助老师给你们提供的素材把它说得更清楚。

预设:拼出的长方形和原平行四边形面积相等,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高,因为长方形的面积等于长×宽,所以平行四边形的面积﹦底×高;
【师梳理】我们一起来梳理一下,看到底要几句话才能把推导过程说明白。
师:首先,要找到它们之间的面积关系(面积相等:长方形的面积=平行四边形面积),接着,我们要分析构成面积的各要素之间的关系(长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高),最后结合公式关系(因为长方形的面积等于长×宽,所以平行四边形的面积﹦底×高)推导得出结论。
(板书:面积关系、要素关系、公式关系)
师:通过对比这三种关系,我们就得出了平行四边形的面积=底×高。(板书:面积公式)
师:根据刚才的梳理,全班一起跟着老师一起来边操作边说一说推导的过程。
同桌之间再边操作边说一说平行四边形面积公式的推导过程。
四、练习巩固,检验目标达成
师:现在,请大家将下面的平行四边形先想象转化成长方形的样子,再算出面积。(独立完成,全班订正)
1. 请先想象转化成长方形,再计算面积。
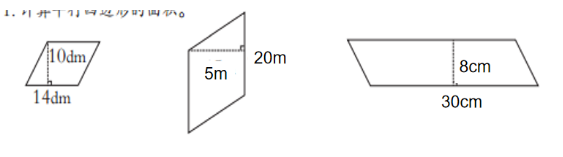
(1)师生一起演示:一起来,第一个先沿高剪,再平移。第二个..第三个..
(2)快速计算,抽生汇报答案。
师评价:看来你们已经会用平行四边形的面积公式进行面积计算了。现在,请你们帮古埃及人算一算平行四边形这块农田有多大?
2.寻找对应底高求面积。(想象转化)
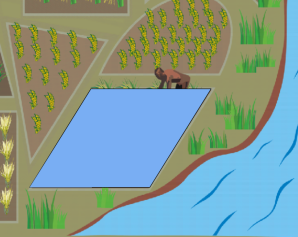
师:你有什么疑惑?(没有数据)
也就是需要数据,是吧?(出示数据)
现在可以计算了吗?为什么?(抽生)
师:我们先来想象一下,如果沿高剪开,再平移,底变到哪去了?底变成了长方形的长了吗?
所以计算平行四边形面积选择数据时底和高必须是?(对应的,互相垂直)
五、全课小结,梳理探究过程
师:今天你有什么收获?在学习方法上你有什么收获?(抽生)
通过这节课的学习,我们知道了以后研究其他的面积,也可以把未知图形转化为已经图形,再由已知图形的面积推导出未知图形的面积计算方法。今天,我们就把长方形的面积也由已知变成了未知,那这个方法能运用到其他图形中吗?比如三角形、梯形的面积公式,可以怎么去探究呢?