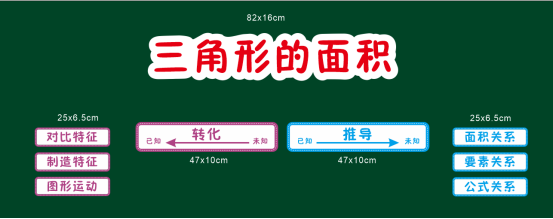
西师版五年级上册第五单元《多边形面积的计算》单元重构
多边形面积的计算
——第二课时(新授课:三角形的面积)
教学目标:
1.能迁移运用平行四边形转化为长方形的方法,将三角形转化为平行四边形或长方形,并能讲清楚转化的过程与理由,发展学生的空间观念。
2.通过对比分析,找到转化前后图形的联系,并推导出三角形的面积公式,发展学生的推理意识。
教学重难点:
重点:能将三角形转化为平行四边形或长方形,推导出三角形的面积公式,并能讲清楚理由。
难点:能将三角形转化为平行四边形或长方形,并能讲清楚转化的过程与理由。
教学准备:
课件、导学单、学具三角形若干。
课前介绍:
学具:课桌左上角2个一样的三角形,在探究过程中可以利用一个或者两个,如果操作中有损坏,可以找老师领取。
教学过程:
一、谈话引入,回顾转化方法
师:同学们,上节课我们研究了平行四边形的面积,把未知图形转化为已知图形,还记得我们是怎么转化的吗?(ppt呈现转化的图片+板书)
生:把平行四边形转化为长方形,沿平行四边形的高剪开,再平移就成了长方形。
师:看来,大家是先对比转化前后图形的特征,再在新图形上制造出旧图形的特征(比如直角),然后沿高剪,再通过图形的平移运动,就实现了转化。(副板书:对比特征、制造特征、图形运动)
师:转化后,我们是怎样推导出平行四边形的面积公式呢?
生:它们面积相等。平行四边形的底=长方形的长,平行四边形的高=长方形的高,所以平行四边形的面积=底×高。
师:看来,我们只要厘清新旧图形间的面积关系、要素关系,就能推导出新图形的面积公式。请同学们试着说一说推导过程。(ppt呈现:推导过程动图+板书关键词:面积关系、要素关系、公式关系)
师:今天我们将再次经历转化和推导的过程来探究三角形的面积。(板书课题:三角形的面积)
二、对比特征,转化成已知图形
师:你想把三角形转化成什么旧图形?
生:平行四边形(或长方形、正方形)
师:你们的想法都不错,我们来验证一下。请看自学要求。
【自学要求】(ppt呈现:注意关键字词加粗、换颜色)
独立思考:
1.你想转化成的图形,它有什么特征?
2.对比特征,怎样将三角形转化成你想要的图形?
(先出示1,2步,独立思考10秒后,再出示3)
3.制造特征,完成转化。利用学具画一画、剪一剪或拼一拼。(你可以借助一个或两个三角形)
(不够的可以找老师领取)
师:大家都有了自己的想法,接下来请看互学要求,请你读。
【互学要求】
1.有序交流自学的两个问题。
①你想转化成的图形,它有什么特征?
②怎样将三角形转化成你想要的图形?(边说边操作)
2.汇总意见,合理分工,准备展示。
(1人汇报问题①,1人汇报问题②,1人操作演示,1人主持/总结/补充)
(教师抽小组上台展示,再借助教具边说边摆,教师准备4个三角形)
答案预设:

师追问:你把两个完全一样的三角形拼成平行四边形是抓住平行四边形的什么特征?(生:平行线、对边平行且相等)
师(补充):也就是说,用两个完全一样的三角形就可以制造这样的特征。
师:和这种方法相同的,请举手。大家有质疑补充吗?
生1:把短边或斜边拼在一起。
师:他们都是抓住了对边相等这个特征,最后都拼成了平行四边形。还有其他的拼法吗?
生2(补充):(教师板书三角形的阴影)
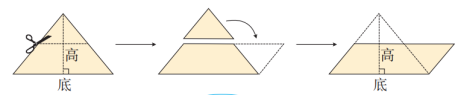
师追问:你是怎么想到要沿三角形两边中点的连线剪开的?
(生:要转化成平行四边形,对边要相等,所以就要沿两边的中点剪,就能保证这两段长度相等,这两段长度也相等(教师手势),这样旋转下来才能刚好拼成平行四边形)
师(补充):哦,沿两边中点剪开就能保证这两段长度相等,旋转下来就能拼成对边相等的平行四边形。
师小结:通过刚才的学习,我们对比了三角形和平行四边形的特征,接着就要想办法制造特征,这两种方法(两个拼、旋转拼)都是制造了平行且相等的对边,最后,通过图形的运动把它转化成了平行四边形。(教师手指3个转化步骤,进行梳理)
师:刚才在操作过程中,我看到有些孩子把两个相同的三角形转来转去都没成功,老师有个小妙招,想学吗?请拿出两个完全一样的三角形,不够的可以从抽屉里面拿。
师(操作步骤):先将两个三角形完全重合,将其中一个三角形绕任意一顶点旋转180°,最后进行平移,使两边重合。大家再试试看。
师:刚才我们只操作了锐角三角形,那如果是直角、钝角三角形呢,还能转化成平行四边形吗?
师:现在请闭上眼睛,在脑袋里任意想象一个三角形,再想一个和它一样的三角形,边想边用手比划(先绕任意一顶点旋转180°,再平移使两边重合),它就拼成了一个平行四边形。成功了吗?跟你想象得一样吗?(PPT演示动画:直角、钝角三角形)
师:请再闭上眼睛边想边比划一下,还是这个三角形,沿两边的中点剪开,再旋转下来,拼成了一个平行四边形,想好了吗?看一看,和你想的一样吗?
得出结论:所以,我们可以得出结论,任意三角形都可以转化成平行四边形。
三、新旧关联,推导面积公式
师:看来大家对三角形转化成平行四边形有了一定的了解,接下来我们就开始推导三角形的面积计算公式吧。请大家拿出抽屉里面的导学单。
【自学要求】
请将导学单中方法一的推导过程补充完整。(学有余力的孩子可以尝试完成方法二的推导过程)
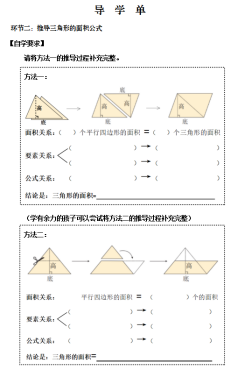
【互学要求】(教师手机拍照学生导学单内容)
1.有序交流你推导的过程。
2.汇总意见,准备展示。
答案预设:
生1:拼成的平行四边形的面积是三角形面积的两倍,平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,平行四边形的面积等于底乘高,所以三角形的面积等于底乘高除以2。(教师相机贴板书)
师追问:针对方法一,你们还有什么质疑或补充吗?(教师相机、补充,教师PPT演示方法一)
师:方法二有完成的吗?
生2:拼成的平行四边形的面积等于三角形的面积,平行四边形的底等于三角形的底,平行四边形的高等于三角形的高的一半,平行四边形的面积等于底乘高的一半,所以三角形的面积等于底乘高的一半。
师追问:那方法二你们有什么质疑或补充吗?(教师相机补充、纠正)
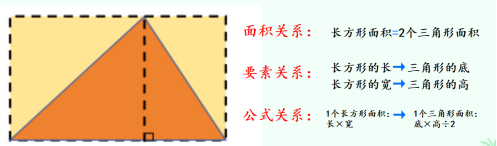
师:刚才我们的推导过程其实都是通过对比分析转化前后的图形,先找到了面积之间的关系,再分析了要素关系,最后结合公式关系推出了三角形的面积公式就是底×高÷2。(形成板书。)
师:现在,请大家同桌之间选择一种方法讲一讲推导的过程。
四、练习巩固,检验目标达成
师:看来同学们已经掌握了三角形面积的转化和推导过程,那接下来我们就来检验一下。
1. 先想象转化成平行四边形,再计算三角形的面积。
(相机纠正学生单位问题)
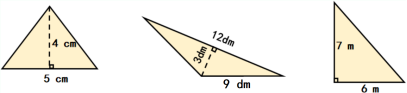
2. 测量数据并计算三角形的面积。(测量结果保留整厘米数)

3. 谁说的对。
小狗:两个三角形一定能拼成平行四边形
小鸟:三角形面积一定比平行四边形面积小
小猴:两个形状一样、大小相等的三角形,能拼成一个平行四边形。
五、全课小结,梳理探究过程
师:同学们,通过今天这节课你有什么收获?
我们以后研究多边形的面积,通常可以先对比特征进行转化,再对比新旧图形之间的对应关系,从已知到未知进行公式推导。
课堂弹性练习内容
今天还有人猜测三角形可以转化成长方形来推导面积,我们一起来看看这种转化方法,你能借助今天所学的知识利用这种转化方法推导出三角形的面积公式吗,你可以把推导过程写在导学单的背面。
六、板书设计