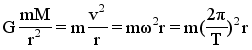导入新课

在初中，我们已经知道物体的质量可以用天平来测量，生活中物体的质量常用电子秤或台秤来称量。

出示图片：天平、电子秤、台秤

阿基米德曾说过：“给我一个支点，我就能撬起整个地球。”

出示图片：阿基米德撬起整个地球

那么如果给你一个足够长的杠杆或足够大的天平你是否就可以称量地球的质量了呢？

不可以。

对于地球，我们怎样“称量”它的质量呢？

观察图片积极讨论思考：对于地球，我们怎样“称量”它的质量呢？

创设情境，激发学习兴趣。

讲授新课

一、“称量”地球的质量

上一节我们学习了万有引力定律：，这一节我们就来学习怎样利用它来算出下面地球的质量。

思考讨论：计算地球的质量时，我们应选择哪个物体作为研究对象？运用哪些物理规律？需要忽略的次要因素是什么？

出示图片：地球

如图以地球表面物体为研究对象，物体m在纬度为θ的位置，万有引力指向地心，它可分解为两个分力：m随地球自转围绕地轴运动的向心力Fn和重力G。

实际上随地球自转的物体向心力远小于重力，在忽略自转的影响下万有引力大小近似等于重力大小。

1、计算地球质量

不考虑地球自转的影响，地面上质量为m的物体所受的重力mg等于地球对物体的引力，即：

m地是地球的质量；R是地球的半径，也就是物体到地心的距离。由此解出：

已知重力加速度g=9．8m/s2，地球半径R=6．4×106m，引力常量G=6．67×10-11N·m2/kg2，试估算地球的质量。

解：

答：地球的质量约为6×1024kg

地面的重力加速度g和地球半径R在卡文迪什之前就已知道，一旦测得引力常量G，就可以算出地球的质量m地。因此，卡文迪什把他自己的实验说成是“称量地球的重量”。

出示图片：卡文迪什

二、计算天体的质量

应用万有引力可算出地球的质量，能否算出太阳的质量呢？

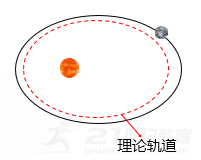
1、基本思路

（1）简化模型：将行星绕太阳的运动看成是匀速圆周运动。

（2）万有引力充当向心力F引=Fn

（3）依据万有引力定律和牛顿第二定律列出方程，从中解出太阳的质量。

设m太是太阳的质量，m是某个行星的质量，r是行星与太阳之间的距离。

解：万有引力充当向心力：

行星运动的角速度ω不能直接测出，但可测出它的周期T。把ω和T的关系

代入上式得到：

得：

思考讨论：该表达式与环行天体质量m有没有关系？

测出行星的公转周期T和它与太阳的距离r，就可以算出太阳的质量，与环行天体质量m无关。只能求出中心天体的质量。

思考讨论：已知太阳与地球间的平均距离约为1．5×1011m，你能估算太阳的质量吗？换用其他行星的相关数据进行估算，结果会相近吗？为什么？

解：

换用其他行星的相关数据进行估算，结果会相近。

虽然不同行星与太阳间的距离r和绕太阳公转的周期T各不相同，但是根据开普勒第三定律，所有行星的均相同，所以无论选择哪颗行星的轨道半径和公转周期进行计算，所得的太阳质量均相同。

思考讨论：怎样计算木星的质量和月球的质量？

要计算木星的质量，对木星的卫星进行测量，只要测得一颗卫星的轨道半径和周期，就可计算木星的质量。

出示图片：木星和它的卫星

要计算月球的质量，由于人类发射的航天器会环绕月球运行，只要测得航天器绕月运行的轨道半径和周期，就可计算月球的质量。

三、计算天体的密度

1、已知太阳某行星的公转周期T、轨道半径r，太阳的半径R，求太阳的密度？

解：由得

①

②

③

把①②代入③得：

2、已知地球的一颗近地卫星做匀速圆周运动的周期为T1，已知引力常数为G，则该天体的密度为多少？若这颗卫星距轨道半径r，测得在该处做匀速圆周运动的周期为T2，则地球的密度怎样表示呢？

解（1）

则：

地球的体积：

（2）由得：

四、发现未知天体

1、海王星的发现

1781年由英国物理学家威廉。赫歇尔发现了天王星，但人们观测到的天王星的运动轨道有些“古怪”：根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。

1945年英国的剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶根据天王星的观测资料，各自独立地利用万有引力定律计算出这颗“新”行星的轨道各自独立计算出来。

1846年9月23日晚，德国的伽勒在勒维耶预言的位置附近发现了这颗行星，人们称其为“笔尖下发现的行星”。后来，这颗行星被命名为海王星。

出示图片：笔尖下发现的行星—海王星

2、海王星的发现的意义

海王星的发现过程充分显示了理论对于实践的巨大指导作用，所用的“计算、预测和观察”的方法指导人们寻找新的天体。

近100年来，人们在这里发现了冥王星、阋神星等几个较大的天体。

出示图片：冥王星、阋神星

五、预言哈雷彗星回归

在牛顿之前，彗星被看作是一种神秘的现象。

出示图片：哈雷彗星

英国天文学家哈雷依据万有引力定律，他大胆预言，彗星周期约为76年，并预言它将于1758年底或1759年初再次回归。1759年3月这颗彗星如期通过了近日点，它最近一次回归是1986年，它的下次回归将在2061年左右。

海王星的发现和哈雷彗星的“按时回归”确立了万有引力定律的地位，也成为科学史上的美谈。

牛顿还用月球和太阳的万有引力解释了潮汐现象，用万有引力定律和其他力学定律，推测地球呈赤道处略为隆起的扁平形状。万有引力定律可以用于分析地球表面重力加速度微小差异的原因，以及指导重力探矿。

课堂练习

1．随着太空技术的飞速发展，人类登陆其它星球成为可能。假设未来的某一天，宇航员登上某一星球后，测得该星球质量是地球质量的8倍，而该星球的平均密度与地球的相等，则该星球表面的重力加速度是地球表面重力加速度的（    ）

A．0.5倍B．2倍C．4倍D．8倍

答案：B

2、（多选题）航天飞机在围绕地球做匀速圆周运动过程中，下列关于宇航员的说法中正确（    ）

A．宇航员不再受重力作用

B．宇航员受的重力提供其做匀速圆周运动的向心力

C．宇航员处于完全失重状态

D．宇航员对座椅的压力为零

答案：BCD

3、我国航天事业取得的巨大成就。已知地球的质量为M，引力常量为G，设“神舟”飞船绕地球做匀速圆周运动的轨道半径为r，则飞船在圆轨道上运行的速率为（    ）

A．B．C．

D．

答案：A

拓展提高

1、2018年12月8日，我国发射的“嫦娥四号”探测器成功升空，并于2019年1月3日实现了人造探测器首次在月球背面软着陆。在探测器逐渐远离地球，飞向月球的过程中（    ）

A．地球对探测器的引力增大

B．地球对探测器的引力减小

C．月球对探测器的引力减小

D．月球对探测器的引力不变

答案：B

2、2019年1月3日，“嫦娥四号”成功软着陆在月球背面，并通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图，揭开了古老月背的神秘面纱。飞船在月球表面软着陆之前，在靠近月球表面的轨道上运行，若要估算月球的平均密度，唯一要测量的物理量是（    ）

A．飞船的轨道半径B．月球的半径

C．飞船的飞行周期D．飞船的线速度

答案：C

3、若地球半径减小1%，而其质量不变，则地球表面重力加速度g的变化情况是——————（填“增大”、“减小”、“不变”），增减的百分比为————%。（取一位有效数字）。

答案：增大；2．

4．两个行星质量分别为m1和m2，绕太阳运行的轨道半径分别是r1和r2，则它们与太阳间的万有引力之比为————，它们的公转周期之比——————。

答案：，

学生阅读课文并思考讨论

学生推导出地球质量的表达式，在练习本上进行定量计算。

学生思考讨论并说出基本思路

学生推导出太阳质量的表达式，在练习本上进行定量计算。

学生思考讨论

学生思考讨论并计算太阳的质量

学生思考讨论：怎样计算木星的质量和月球的质量？

在教师的引导下求太阳的密度？

学生思考讨论并计算地球的密度

学生阅读课文并发表自己的看法。

学生阅读课文

预言哈雷彗星回归。

学生练习

明确在忽略自转的影响下万有引力大小近似等于重力大小。

锻炼学生的计算能力，规范解题步骤

锻炼学生的总结以及语言表达能力，为下面的计算做铺垫

锻炼学生的计算能力，规范解题步骤

明确中心天体的质量与环行天体质量m无关。

锻炼学生的计算能力并让学生明白换用其他行星的相关数据进行估算结果不会改变。

巩固测量中心天体的方法。

锻炼学生的推导能力，掌握计算天体密度的方法

明确近地卫星和距地面有一定高度的卫星，地球的密度的不同表达式。

通过万有引力定律成功地预测未知的星体，这不仅巩固了万有引力定律的地位，也充分展示了科学理论的预见性。

锻炼学生的自主学习能力

巩固本节的知识

课堂小结

课堂总结

1、中心天体的质量与环行天体质量m无关，且只能求出中心天体的质量。

2、解决天体问题的两条思路

第一种思路：重力等于物体与天体间的万有引力

第二种思路：万有引力充当向心力

梳理自己本节所学知识进行交流

根据学生表述，查漏补缺，并有针对性地进行讲解补充。

板书

一、“称量”地球的质量

得：

二、计算天体的质量

得：

只能求出中心天体的质量。

三、计算天体的密度

四、发现未知天体